Advertisements
Advertisements
Question
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
Solution
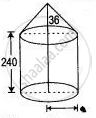
Let r1 cm and r2 cm denote the radii of the base of the cylinder and cone respectively. Then,
r1 = r2 = 8 cm
Let h1 and h2 cm be the height of the cylinder and the cone respectively. Then,
h1 = 240 cm and h2 = 36 cm.
Now, Volume of the cylinder = `πr_1^2h_1` cm3
= (π x 8 x 8 x 240 ) cm3
= (π x 64 x 240 ) cm3
Volume of the cone = `1/3 πr_2^2h_2` cm3
= `(1/3 π xx 8 xx 8 xx 36 )` cm3
= `(1/3 π xx 64 xx 36 )` cm3
∴ Total volume of iron = Volume of the cylinder + Volume of the cone
= `(π xx 64 xx 240 + 1/3 π xx 64 xx 36)` cm3
= ` π xx 64 xx (240 + 12)` cm3
= `22/7 xx 64 xx 252` cm3
= 22 x 64 x 36 cm3
Hence, total weight of the pillar = Volume x weight per cm3
= ( 22 x 64 x 36 ) x 7.8 gms
= 395366.4 gms
= 395.3664 kg.
APPEARS IN
RELATED QUESTIONS
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

A spherical glass vessel has a cylindrical neck 8 cm long, 2cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
A reservoir in the form of the frustum of a right circular cone contains 44 × 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: π = 22/7)
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
The rain water from a 22 m × 20 m roof drains into a cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills `4/5` th of the cylindrical vessel, then find the rainfall in centimetre.
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic cm of iron weighs 7.5 g, find the weight of the box.
