Advertisements
Advertisements
Question
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
Solution
Let r and h be radius and height of the cone respectively.
Radius of cone (r) = 7 cm (Given)
Diameter of cone = 2 × r = (2 × 7) cm = 14 cm
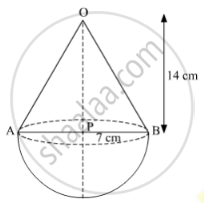
According to the question, height of the cone is equal to its diameter.
∴ Height of cone (h) = 14 cm
Radius of hemisphere = Radius of cone = 7 cm
∴ Volume of solid = Volume of cone + Volume of hemisphere
`=1/3pir^2h+2/3pir^3`
`=(pir^2)/3[h+2r]`
`=1/3xx22/7xx7xx7xx[14+(2xx7)]cm^2`
`=22/3xx7xx28cm^3`
`=4312/2cm^2`
`=1437.33cm^3`
Thus, the volume of the solid is 1437.33 cm3.
APPEARS IN
RELATED QUESTIONS
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
A rectangular tank 15m long and 11m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5m. Find least height of tank that will serve purpose .
The difference between outer and inner curved surface areas of a hollow right circular cylinder 14cm long is 88cm2. If the volume of metal used in making cylinder is 176cm3.find the outer and inner diameters of the cylinder____?
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
A copper rod of diameter 2 cm and length 10 cm is drawn into a wire of uniform thickness and length 10 m. Find the thickness of the wire.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 mins; if 8 cm standing water is needed?
The volume (in cm3) of the largest right circular cone that can be cut off from a cube of edge 4.2 cm is ______.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
The largest sphere is carved out of a solid cube of side 21 cm. Find the volume of the sphere.
A solid is in the shape of a cone standing on a hemisphere with both their diameters being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid. [Use π = 3.14]
