Advertisements
Advertisements
Question
A copper rod of diameter 2 cm and length 10 cm is drawn into a wire of uniform thickness and length 10 m. Find the thickness of the wire.
Solution
We have,
the radius of the copper rod, `R = 2/2 =1 "cm"`
the height of the copper rod , H = 10 cm and
the height of the wire, h = 10m = 1000 cm
Let the radius of the wire be r.
As,
Volume of the wire= Volume of the rod
`rArr pir^2h = piR^2H`
`rArr r^2h = R^2H`
`rArr r^2 xx 1000 = 1xx10`
`rArr r^2 = 10/100`
`rArr r^2 = 1/100`
`rArr r= sqrt(1/100)`
`rArr r = 1/10`
`rArr r=0.1 "cm"`
⇒ The diameter of the wire = 2r = 2 × 0.1 = 0.2 cm
∴ The thickness of the wire = 0.2 cm
So, the thickness of the wire is 0.2 cm or 2 mm.
APPEARS IN
RELATED QUESTIONS
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
A copper rod of diameter 1cm and length 8cm is drawn into a wire of length 18m of uniform thickness. Find thickness of wire?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
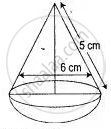
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.
A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
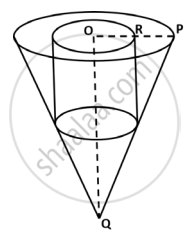
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)