Advertisements
Advertisements
प्रश्न
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
उत्तर
Let r and h be radius and height of the cone respectively.
Radius of cone (r) = 7 cm (Given)
Diameter of cone = 2 × r = (2 × 7) cm = 14 cm
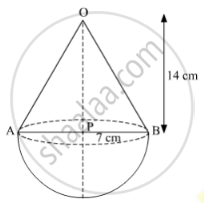
According to the question, height of the cone is equal to its diameter.
∴ Height of cone (h) = 14 cm
Radius of hemisphere = Radius of cone = 7 cm
∴ Volume of solid = Volume of cone + Volume of hemisphere
`=1/3pir^2h+2/3pir^3`
`=(pir^2)/3[h+2r]`
`=1/3xx22/7xx7xx7xx[14+(2xx7)]cm^2`
`=22/3xx7xx28cm^3`
`=4312/2cm^2`
`=1437.33cm^3`
Thus, the volume of the solid is 1437.33 cm3.
APPEARS IN
संबंधित प्रश्न
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
500 persons have to dip in a rectangular tank which is 80m long and 50m broad. What is the rise in the level of water in the tank, if the average displacement of water by a person is 0.04m3 .
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7`litres per sec.
How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
The volumes of two cubes are in the ratio 1 : 27. The ratio of their surface area is
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).
In a swimming pool measuring 90 m × 40 m, 150 men take a dip. If the average displacement of water by a man is 8 m3, then rise in water level is ______.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
