Advertisements
Advertisements
प्रश्न
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
उत्तर
Given that volume of a hemisphere`=2424(1)/2cm^3`
Volume of a hemisphere`=2/3pir^3`
⇒ `2/3pir^3=2425(1)/2`
⇒`2/3pir^3=4841/2`
⇒ `r^3=(4851xx3)/(2xx2xxpi)`
⇒ `r^3=(4851xx3)/(4pi)`
r3
r = 10.50cm
∴ Radius of hemisphere = 10.5cm
Curved surface area of hemisphere = 2πr2
= 2π(10.5)2
=692.72
⇒693cm2
∴curved surface area off hemisphere = 693cm2
APPEARS IN
संबंधित प्रश्न
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
A conical flask is full of water. The flask has base radius r and height h. The water is poured into a cylindrical flask of base-radius mr. Find the height of water in the cylindrical flask.
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed (Use it =`22/7`)
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
Match the following columns:
| Column I | Column II |
| (a) A solid metallic sphere of radius 8 cm is melted and the material is used to make solid right cones with height 4 cm and base radius of 8 cm. How many cones are formed? | (p) 18 |
| (b) A 20-m-deep well with diameter 14 m is dug up and the earth from digging is evenly spread out to form a platform 44 m by 14 m. The height of the platform is ...........m. |
(q) 8 |
| (c) A sphere of radius 6 cm is melted and recast in the shape of a cylinder of radius 4 cm. Then, the height of the cylinder is ......... cm. |
(r) 16 : 9 |
| (d) The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ....... . |
(s) 5 |
In the given figure, find the area of the unshaded portion within the rectangle. (Take π = 22/7).
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Read the following passage and answer the questions given below.
|
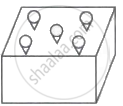
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.