Advertisements
Advertisements
प्रश्न
Read the following passage and answer the questions given below.
|
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.
उत्तर
1. Since,
Volume of cone = `1/3 πr^2h`
Here, r = 2.1 cm and h = 6 cm
∴ Volume of 5 conical cavities = `5 xx 1/3 πr^2h`
= `5 xx 1/3 xx 22/7 xx (2.1)^2 xx 6`
= `(5 xx 22 xx 2.1 xx 2.1 xx 6)/(3 xx 7)`
= `2910.6/21`
= 138.6 cm3
2. Volume of the wood in the final product = Volume of cuboidal log of wood – Volume of five conical cavities
= (10 × 10 × 8) – 138.6
= 800 – 138.6 ...[∵ Volume of cuboid = l × b × h]
= 661.4 cm3
APPEARS IN
संबंधित प्रश्न
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42cm and height 21cm which are filled completely. Find the diameter of cylindrical vessel?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.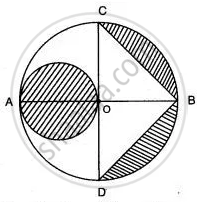
Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
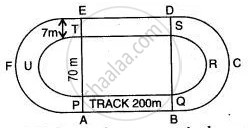
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
A metallic hollow cylindrical pipe has outer and inner radii as 6 cm and 4 cm respectively. Find the volume of the metal used in the pipe of length of 14 cm.