Advertisements
Advertisements
Question
Read the following passage and answer the questions given below.
|
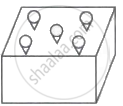
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.
Solution
1. Since,
Volume of cone = `1/3 πr^2h`
Here, r = 2.1 cm and h = 6 cm
∴ Volume of 5 conical cavities = `5 xx 1/3 πr^2h`
= `5 xx 1/3 xx 22/7 xx (2.1)^2 xx 6`
= `(5 xx 22 xx 2.1 xx 2.1 xx 6)/(3 xx 7)`
= `2910.6/21`
= 138.6 cm3
2. Volume of the wood in the final product = Volume of cuboidal log of wood – Volume of five conical cavities
= (10 × 10 × 8) – 138.6
= 800 – 138.6 ...[∵ Volume of cuboid = l × b × h]
= 661.4 cm3
APPEARS IN
RELATED QUESTIONS
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
Two cubes each of volume 125 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A well 28.8 m deep and of diameter 2 m is dug up. The soil dug out is spread all around the well to make a platform 1 m high considering the fact losse soil settled to a height in the ratio 6 : 5 find the width of the platform.
The volumes of two spheres are in the ratio 27 : 8. The ratio of their curved surface is ______.
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r) : r is ______.
In a swimming pool measuring 90 m × 40 m, 150 men take a dip. If the average displacement of water by a man is 8 m3, then rise in water level is ______.
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.