Advertisements
Advertisements
Question
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
Solution
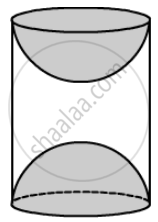
We have,
Radius of the cylinder = Radius of the hemispher = r = 3.5 cm and
Height of the cylinder, h = 10 cm
Now,
Volume of the toy = Volume of the cylinder - Volume of the two hemispheres
`= pi"r"^2"h"-2xx2/3pi"r"^3`
`=pi"r"^2("h" - (4"r")/3)`
`= 22/7xx3.5xx3.5xx(10-(4xx3.5)/(3))`
`=38.5xx(10-14/3)`
`=38.5xx16/3`
`=616/3 "cm"^3`
≈ 205.33 cm3
So, the volume of wood in the toy is `616/3` cm3 or 205.33 cm3
APPEARS IN
RELATED QUESTIONS
A spherical ball of radius 3cm is melted and recast into three spherical balls. The radii of the two of balls are 1.5cm and 2cm . Determine the diameter of the third ball?
A rectangular tank 15m long and 11m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5m. Find least height of tank that will serve purpose .
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
The sum of the radius of the base and the height of a solid cylinder is 37 metres. If the total surface area of the cylinder be 1628 sq metres, then find its volume.
The rain water from a 22 m × 20 m roof drains into a cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills `4/5` th of the cylindrical vessel, then find the rainfall in centimetre.
The volume of a right circular cylinder with its height equal to the radius is `25"1"/7` cm3. Find the height of the cylinder.
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
A metallic solid right circular cone is of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the
diameter of the sphere.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
