Advertisements
Advertisements
प्रश्न
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
उत्तर
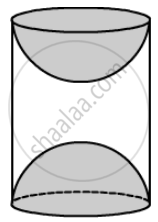
We have,
Radius of the cylinder = Radius of the hemispher = r = 3.5 cm and
Height of the cylinder, h = 10 cm
Now,
Volume of the toy = Volume of the cylinder - Volume of the two hemispheres
`= pi"r"^2"h"-2xx2/3pi"r"^3`
`=pi"r"^2("h" - (4"r")/3)`
`= 22/7xx3.5xx3.5xx(10-(4xx3.5)/(3))`
`=38.5xx(10-14/3)`
`=38.5xx16/3`
`=616/3 "cm"^3`
≈ 205.33 cm3
So, the volume of wood in the toy is `616/3` cm3 or 205.33 cm3
APPEARS IN
संबंधित प्रश्न
A conical flask is full of water. The flask has base radius r and height h. The water is poured into a cylindrical flask of base-radius mr. Find the height of water in the cylindrical flask.
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.
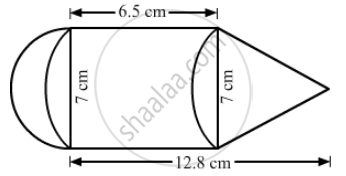
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
The diameter of a sphere is 14 cm. Its volume is
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
