Advertisements
Advertisements
प्रश्न
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
उत्तर
We have,
Radius of the metallic cone, r = 12 cm,
Height of the metallic cone, h = 24 cm and
Radiusof the sphere, R = 2 cm
Now,
The number of spheres so formed`= "Volume of the metallic cone"/"Volume of a sphere" `
`= ((1/3pi"r"^2"h"))/((4/3pi"R"^3))`
`= ("r"^2"h")/(4"R"^3)`
`=(12xx12xx24)/(4xx2xx2xx2)`
= 108
So, the number of spheres so formed is 108.
APPEARS IN
संबंधित प्रश्न
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
The largest sphere is to be curved out of a right circular of radius 7cm and height 14cm. find volume of sphere?
A copper rod of diameter 1cm and length 8cm is drawn into a wire of length 18m of uniform thickness. Find thickness of wire?
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 mins; if 8 cm standing water is needed?
A well 28.8 m deep and of diameter 2 m is dug up. The soil dug out is spread all around the well to make a platform 1 m high considering the fact losse soil settled to a height in the ratio 6 : 5 find the width of the platform.
In the given figure, find the area of the unshaded portion within the rectangle. (Take π = 22/7).
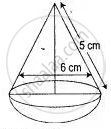
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
