Advertisements
Advertisements
प्रश्न
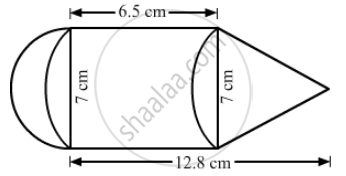
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
उत्तर
Diameter of the cylindrical part =7 cm
Therefore,radius of the cylindrical part = 3.5 cm
Volume of hemisphere `= 2/3pir^3 = 2/3xx22/7xx3.5xx3.5xx3.5 = 89.83 "cm"^3`
Volume of the cylinder`= pir^2h =22/7xx3.5xx3.5xx6.5 = 250.25 "cm"^3`
Height of cone
= 12.8 - 6.5 = 6.3 cm
Volume of the cone `=1/3pir^2h =1/3xx22/7xx3.5xx3.5xx6.3 = 80.85 "cm"^3`
Total volume `= 89.83 + 250.25 + 80.85 = 420.93 "cm"^3`
APPEARS IN
संबंधित प्रश्न
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball of radius 9cm is dropped into the tube and thus level of water is raised by hcm. What is the value of h.
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
12 spheres of the same size are made from melting a solid cylinder of 16 cm diameter and 2 cm height. The diameter of each sphere is
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm, containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume of water
- displaced out of the cylinder
- left in the cylinder.
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)