Advertisements
Advertisements
प्रश्न
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
उत्तर
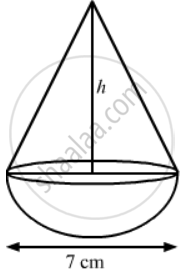
We have,
Base radius of cone = Base radius of hemisphere `= r = 7/2 = 3.5` cm,
As, the volume of cone + Volume of hemisphere = 231
`rArr 1/3 pir^2h + 2/3pir^3 = 231`
`rArr 1/3 pir^2 (h + 2r) = 231`
`rArr 1/3 xx 22/7xx3.5xx3.5xx(h + 2xx 3.5) = 231`
`rArr 38.5/3 xx (h + 7) =231`
`rArr h + 7 = 231xx3/38.5`
`rArr h +7 = 18`
` rArr h = 18-7`
`rArr h=11 cm`
so, the hieght of the toy = h + r = 11 + 3.5 = 14.5 cm
APPEARS IN
संबंधित प्रश्न
A solid toy is in the form of a hemisphere surmounted by a right circular cone. height of the cone is 2 cm and the diameter of the base is 4 cm. If a right circular cylinder circumscribes the toy, find how much more space it will cover.
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
Find the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and `1/8` space of the cube remains unfilled. Number of marbles required is
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m calculate the length of the canvas which is 5m wide to make the required tent.
The volumes of two spheres are in the ratio 27 : 8. The ratio of their curved surface is ______.
A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is ______.
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
Find the volume of a solid hemisphere whose total surface area is 462 sq.m.
