Advertisements
Advertisements
Question
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
Solution
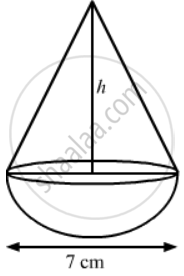
We have,
Base radius of cone = Base radius of hemisphere `= r = 7/2 = 3.5` cm,
As, the volume of cone + Volume of hemisphere = 231
`rArr 1/3 pir^2h + 2/3pir^3 = 231`
`rArr 1/3 pir^2 (h + 2r) = 231`
`rArr 1/3 xx 22/7xx3.5xx3.5xx(h + 2xx 3.5) = 231`
`rArr 38.5/3 xx (h + 7) =231`
`rArr h + 7 = 231xx3/38.5`
`rArr h +7 = 18`
` rArr h = 18-7`
`rArr h=11 cm`
so, the hieght of the toy = h + r = 11 + 3.5 = 14.5 cm
APPEARS IN
RELATED QUESTIONS
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
The diameter of a metallic sphere is equal to 9cm. it is melted and drawn into a long wire of diameter 2mm having uniform cross-section. Find the length of the wire?
The diameters of internal and external surfaces of hollow spherical shell are 10cm and 6cm respectively. If it is melted and recast into a solid cylinder of length of 2`2/3`cm, find the
diameter of the cylinder.
A bucket made up of a metal sheet is in form of a frustum of cone of height 16cm with diameters of its lower and upper ends as 16cm and 40cm. find the volume of bucket. Also find cost of bucket if the cost of metal sheet used is Rs 20 per 100 cm2
The radii of two cylinders are in the ratio 3 : 5. If their heights are in the ratio 2 : 3, then the ratio of their curved surface areas is
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
In the given figure, find the area of the unshaded portion within the rectangle. (Take π = 22/7).
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
A solid iron cuboidal block of dimensions 4.4 m × 2.6 m × 1 m is recast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
From a soild cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid.
