Advertisements
Advertisements
Question
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
Solution
We have
the base radius of the cylindrical containers, R=6 cm,
the height of the container, H = 15 cm,
Let the base radius and the height of the ice-cream cone be r an
Also, h = 4r
Now, the volume of the cylindrical container = πR2H
`= 22/7xx6xx6xx15`
`= 11880/7` cm3
`rArr "the volume of the ice -cream distributed to 10 children" = 11880/7 cm`
`rArr 10xx "Volume of a ice - creame cone = 11880/7" `
`rArr 10xx ("Volume of the cone + Volume of the hemisphere") = 11880/7`
`rArr 10xx(1/3 pir^2h + 2/3 pir^3) = 11880/7`
`rArr 10xx(1/3pir^2hxx4r + 2/3pir^3)= 11880/7`
`rArr 10xx(1/3pir^2xx4r+2/3pir^3)= 11880/7`
`rArr 10xx(6/3pir^3)=11880/7`
`rArr 10xx2xx22/7xxr^3 = 11880/7`
`rArr r^3 = (11880xx7)/(7xx10xx2xx22)`
`rArr r^3 = 27`
`rArr r = root(3)(27)`
∴ r = 3 cm
So, the radius of the ice-cream cone is 3 cm.
APPEARS IN
RELATED QUESTIONS
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
How many bags of grain can be stored in a cuboidal granary (8 m × 6 m × 3 m), if each bag occupies a space of 0.64 m3?
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : curved surface area.
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r) : r is ______.
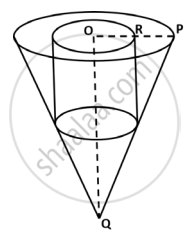
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)