Advertisements
Advertisements
प्रश्न
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
उत्तर
We have
the base radius of the cylindrical containers, R=6 cm,
the height of the container, H = 15 cm,
Let the base radius and the height of the ice-cream cone be r an
Also, h = 4r
Now, the volume of the cylindrical container = πR2H
`= 22/7xx6xx6xx15`
`= 11880/7` cm3
`rArr "the volume of the ice -cream distributed to 10 children" = 11880/7 cm`
`rArr 10xx "Volume of a ice - creame cone = 11880/7" `
`rArr 10xx ("Volume of the cone + Volume of the hemisphere") = 11880/7`
`rArr 10xx(1/3 pir^2h + 2/3 pir^3) = 11880/7`
`rArr 10xx(1/3pir^2hxx4r + 2/3pir^3)= 11880/7`
`rArr 10xx(1/3pir^2xx4r+2/3pir^3)= 11880/7`
`rArr 10xx(6/3pir^3)=11880/7`
`rArr 10xx2xx22/7xxr^3 = 11880/7`
`rArr r^3 = (11880xx7)/(7xx10xx2xx22)`
`rArr r^3 = 27`
`rArr r = root(3)(27)`
∴ r = 3 cm
So, the radius of the ice-cream cone is 3 cm.
APPEARS IN
संबंधित प्रश्न
Water in a canal 1.5m wide and 6m deep is flowering with a speed of 10km/ hr. how much area will it irrigate in 30 minutes if 8cm of standing water is desired?
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is `2/3` of the volume of hemisphere, calculate the height of the cone and the surface area of the toy.
`(use pi = 22/7)`
A copper rod of diameter 2 cm and length 10 cm is drawn into a wire of uniform thickness and length 10 m. Find the thickness of the wire.
A solid piece of iron in the form a cuboid of dimensions (49 cm × 33 cm × 24 cm) is moulded into a solid sphere. The radius of the sphere is ______.
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
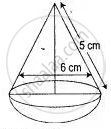
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
A surahi is the combination of ______.
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
