Advertisements
Advertisements
Question
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : curved surface area.
Solution
Curved surface area (Original) of a solid right circular cylinder = 2πrh
= 2π × 100 × 100
= 20000π cm2
Curved surface area (New) of a solid right circular cylinder
= 2πr'h'
= 2π × 80 × 110
= 17600π cm2
Decrease in curved area
= Original CSA – New CSA
= (20000π – 17600π) cm2
= 2400π cm2
Percentage change in curved surface area = `"Decrease in curved surface area"/"Original curved surface area" xx 100%`
= `(2400 pi cm^2)/(20000 pi cm^2) xx 100%`
= 12%
APPEARS IN
RELATED QUESTIONS
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
The diameters of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the value of water (i) displaced out of the cylinder (ii) left in the cylinder. (Take π 22/7)
A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to the brim. How many children will get the ice-cream cones?
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r) : r is ______.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
The rain water from a roof of dimensions 22 m × 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
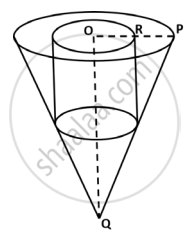
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)