Advertisements
Advertisements
Question
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
Solution
Given, ice-cream cone is the combination of a hemisphere and a cone.
Also, radius of hemisphere = 5 cm
∴ Volume of hemisphere
= `2/3 pi"r"^3`
= `2/3 xx 22/7 xx (5)^3`
= `5500/21`
= 261.90 cm3
Now, radius of the cone = 5 cm
And height of the cone = 10 – 5 = 5 cm
∴ Volume of the cone
= `1/3 pi"r"^2"h"`
= `1/3 xx 22/7 xx (5)^2 xx 5`
= `2750/21`
= 130.95 cm3
Now, total volume of ice-cream cone
= 261.90 + 130.95
= 392.85 cm3
Since, `1/6` part is left unfilled with ice-cream.
∴ Required volume of ice-cream
= `392.85 - 392.85 xx 1/6`
= 392.85 – 65.475
= 327.4 cm3
APPEARS IN
RELATED QUESTIONS
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball of radius 9cm is dropped into the tube and thus level of water is raised by hcm. What is the value of h.
The diameter of a metallic sphere is equal to 9cm. it is melted and drawn into a long wire of diameter 2mm having uniform cross-section. Find the length of the wire?
A petrol tank is a cylinder of base diameter 21 cm and length 18 cm fitted with conical ends each of axis length 9 cm. Determine the capacity of the tank.
A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?
The volume of a right circular cylinder with its height equal to the radius is `25"1"/7` cm3. Find the height of the cylinder.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : curved surface area.
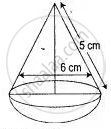
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04m3?
