Advertisements
Advertisements
Question
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder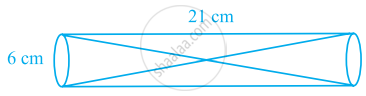
Solution
Let volume of cone A be 2V and volume of cone B be V.
Again, let height of the cone A = h1 cm,
Then height of cone B = (21 – h1) cm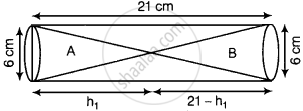
Given, diameter of the cone = 6 cm
∴ Radius of the cone = `6/2` = 3 cm
Now, volume of the cone,
A = 2V
= `1/3 pi"r"^2"h"`
= `1/3 pi(3)^2"h"_1`
⇒ V = `1/6 pi9"h"_1`
= `3/2 "h"_1pi` ...(i)
And volume of the cone,
B = V
= `1/3 pi(3)^2(21 - "h"_1)`
= 3π(21 – h1) ...(ii)
From equations (i) and (ii),
`3/2 "h"_1 pi` = 3π(21 – h1)
⇒ h1 = 2(21 – h1)
⇒ 3h1 = 42
⇒ h1 = `42/3` = 14 cm
∴ Height of cone,
B = 21 – h1
= 21 – 14
= 7 cm
Now, volume of the cone,
A = `3 xx 14 xx 22/7` = 132 cm2 ...[Using equation (i)]
And volume of the cone,
B = `1/3 xx 22/7 xx 9 xx 7` = 66 cm3 ...[Using equation (ii)]
Now, volume of the cylinder
= πr2h
= `22/7 (3)^2 xx 21`
= 594 cm3
∴ Required volume of the remaining portion
= Volume of the cylinder – (Volume of cone A + Volume of cone B)
= 594 – (132 + 66)
= 396 cm3
APPEARS IN
RELATED QUESTIONS
A reservoir in the form of the frustum of a right circular cone contains 44 × 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: π = 22/7)
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
The heights of two circular cylinders of equal volume are in the ratio 1 : 2. The ratio of their radii is
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
If the radius of base of a right circular cylinder is halved, keeping the height same, the ratio of the volume of the reduced cylinder to that of the original cylinder is ______.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
