Advertisements
Advertisements
Question
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
Solution
Radius of hemisphere = 9 cm
Volume of hemisphere `= 2/3 pir^3`
`=(2/3pixx9xx9xx9)"cm"^3`
Radius of each bottle `= 3/2 "cm"`
Height of each bottle = 4 cm
Volume of each bottle `= pi"r"^2"h"`
`=(pixx3/2xx3/2xx4)"cm"^3`
Numbe of bottles `= "Volume of the hemisphre"/"Volume of each bottle"`
`=(2pixx9xx9xx9xx2xx2)/(3xxpixx3xx3xx4)`
= 54
APPEARS IN
RELATED QUESTIONS
A conical flask is full of water. The flask has base radius r and height h. The water is poured into a cylindrical flask of base-radius mr. Find the height of water in the cylindrical flask.
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
Three cubes of a metal whose edges are in the ratio 3 : 4 : 5 are melted and converted into a single cube whose diagonal is `12sqrt(3)` cm. Find the edges of the three cubes.
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
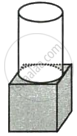
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
The rain water from a roof of dimensions 22 m × 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
The sum of the length, breadth and height of a cuboid is `6sqrt(3)` cm and the length of its diagonal is `2sqrt(3)` cm. The total surface area of the cuboid is ______.
