Advertisements
Advertisements
Question
The rain water from a roof of dimensions 22 m × 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
Solution
Given, length of roof = 22 m
And breadth of roof = 20 m
Let the rainfall be a cm.
∴ Volume of water on the roof = `22 xx 20 xx a/100 = (22a)/5 m^3`
Also, we have radius of base of the cylindrical vessel = 1 m
And height of the cylindrical vessel = 3.5 m
∴ Volume of water in the cylindrical vessel when it is just full
= `(22/7 xx 1 xx 1 xx 7/2)`
= 11 m3
Now, volume of water on the roof = Volume of water in the vessel
⇒ `(22a)/5` = 11
∴ a = `(11 xx 5)/22` = 2.5 ...[∵ Volume of cylinder = π × (radius)2 × height]
Hence, the rainfall is 2.5 cm
APPEARS IN
RELATED QUESTIONS
A spherical ball of radius 3cm is melted and recast into three spherical balls. The radii of the two of balls are 1.5cm and 2cm . Determine the diameter of the third ball?
A hollow sphere of internal and external radii 2cm and 4cm is melted into a cone of basse radius 4cm. find the height and slant height of the cone______?
A solid piece of iron of dimensions 49 × 33 × 24 cm is moulded into a sphere. The radius of the sphere is
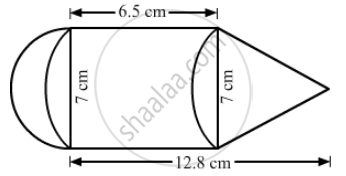
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
A copper sphere of diameter 18 cm is drawn into a wire of diameter 4 mm. Find the length of the wire.
The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm2 and the volume of material in it is 1056 cm3. Find its internal and external radii. Given that the height of the cylinder is 21 cm.
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
