Advertisements
Advertisements
Question
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
Solution
Given that, length of cuboid pen stand (l) = 10 cm
Breadth of cubiod pen stand (b) = 5 cm
And height of cuboid pen stand (h) = 4 cm

∴ Volume of cuboid pen stand
= l × b × h
= 10 × 5 × 4
= 200 cm3
Also, radius of conical depression (r) = 0.5 cm
And height (depth) of a conical depression (h1) = 2.1 cm
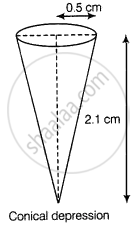
∴ Volume of a conical depression
= `1/3pir^2h_1`
= `1/3 xx 22/7 xx 0.5 xx 0.5 xx 2.1`
= `(22 xx 5 xx 5)/1000`
= `22/40`
= `11/20`
= 0.55 cm3
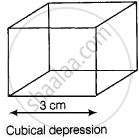
Also, given
Edge of cubical depression (a) = 3 cm
∴ Volume of cubical depression = (a)3 = (3) = 27 cm3
So, volume of 4 conical depressions
= 4 × Volume of a conical depression
= `4 xx 11/20`
= `11/5 cm^3`
Hence, the volume of wood in the entire pen stand
= Volume of cuboid pen stand – Volume of 4 conical depressions – Volume of a cubical depressions
= `200 - 11/5 - 27`
= `200 - 146/5`
= 200 – 29.2
= 170.8 cm3
So, the required volume of the wood in the entire stand is 170.8 cm3.
APPEARS IN
RELATED QUESTIONS
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A well of diameter 2m is dug14m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40cm. Find width of the embankment?
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of \[3\frac{4}{7}\] litre per second. How much time will it take to make the tank half empty?\[\left[ Use \pi = \frac{22}{7} \right]\]
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
A solid is in the shape of a cone standing on a hemisphere with both their diameters being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid. [Use π = 3.14]
