Question

A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.

Answer 1

Given that, length of cuboid pen stand (l) = 10 cm

Breadth of cubiod pen stand (b) = 5 cm

And height of cuboid pen stand (h) = 4 cm

∴ Volume of cuboid pen stand

= l × b × h

= 10 × 5 × 4

= 200 cm³

Also, radius of conical depression (r) = 0.5 cm

And height (depth) of a conical depression (h₁) = 2.1 cm

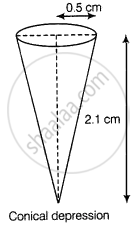
∴ Volume of a conical depression

= `1/3pir^2h_1`

= `1/3 xx 22/7 xx 0.5 xx 0.5 xx 2.1`

= `(22 xx 5 xx 5)/1000`

= `22/40`

= `11/20`

= 0.55 cm³

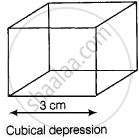
Also, given

Edge of cubical depression (a) = 3 cm

∴ Volume of cubical depression = (a)³ = (3) = 27 cm³ 

So, volume of 4 conical depressions

= 4 × Volume of a conical depression

= `4 xx 11/20`

= `11/5 cm^3`

Hence, the volume of wood in the entire pen stand

= Volume of cuboid pen stand – Volume of 4 conical depressions – Volume of a cubical depressions

= `200 - 11/5 - 27`

= `200 - 146/5`

= 200 – 29.2

= 170.8 cm³

So, the required volume of the wood in the entire stand is 170.8 cm³.