Advertisements
Advertisements
प्रश्न
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass. [Use π = 3.14]
उत्तर
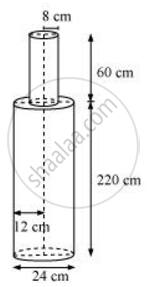
rom the figure, it can be observed that
Height (h1) of larger cylinder = 220 cm
Radius (r1) of larger cylinder = `24/2` = 12 cm
Height (h2) of smaller cylinder = 60 cm
Radius (r2) of smaller cylinder = 8 cm
Total volume of pole = volume of larger cylinder + volume of smaller cylinder
`= pir_1^2h_1+pir_2^2h_2`
`=pi(12)^2xx220+pi(8)^2xx60`
`=pi[144xx220+64xx60]`
= `35520xx3.14`
= 111532.8 cm3
Mass of 1 cm3 iron = 8 g
Mass of 111532.8 cm3 iron
= 111532.8 × 8
= 892262.4 g
= 892.262 kg
APPEARS IN
संबंधित प्रश्न
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A cylindrical jar of radius 6cm contains oil. Iron sphere each of radius 1.5cm are immersed in the oil. How many spheres are necessary to raise level of the oil by two centimetress?
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
A solid iron pole having cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that the mass of 1 cm3of iron is 8 gm.
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume of water
- displaced out of the cylinder
- left in the cylinder.
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is ______.
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 mins; if 8 cm standing water is needed?
If the radius of base of a right circular cylinder is halved, keeping the height same, the ratio of the volume of the reduced cylinder to that of the original cylinder is ______.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
How many bags of grain can be stored in a cuboid granary 12 m × 6 m × 5 m. If each bag occupies a space of 0.48 m3?
A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is ______.
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour?
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
From a soild cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid.
