Advertisements
Advertisements
प्रश्न
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
उत्तर
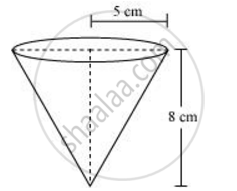
Height (h) of conical vessel = 8 cm
Radius (r1) of conical vessel = 5 cm
Radius (r2) of lead shots = 0.5 cm
Let n number of lead shots were dropped in the vessel.
Volume if water in concial vessel = `1/3 piR^2 h`
= `1/3 xx 22/7 xx (5) xx 8`
= `4400/21`cm3
Now, total volume of lead shots = `1/4` of [volume of water in the cone]
= `1/4 xx 4400/21`
= `1100/21` cm3
Since, radius of spherical lead shot (r)
= 0.5 cm = `5/10`cm3
∴ Volume of one lead shot = `4/3 pi r^3`
= `(4/3 xx 22/7 xx 5/10 xx 5/10 xx 5/10)` cm3
∴ Number of lead shots
= `"Total volume of lead shots"/"Volume of one lead shot"`
= `(1100/21)/((4 xx 22 xx 5 xx 5 xx 5)/(3 xx 7xx 1000))`
= 100
Thus, the required number of lead shorts = 100
APPEARS IN
संबंधित प्रश्न
50 circular plates each of diameter 14cm and thickness 0.5cm are placed one above other to form a right circular cylinder. Find its total surface area?
A hemisphere tool of internal radius 9cm is full of liquid. This liquid is to be filled into
cylindrical shaped small bottles each of diameter 3cm and height 4cm. how many bottles are necessary to empty the bowl.
A farmer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
A hemispherical depression is cut out from one face of a cubical block of side 7 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. [Use π = \[\frac{22}{7}\]]
The sum of the radius of the base and the height of a solid cylinder is 37 metres. If the total surface area of the cylinder be 1628 sq metres, then find its volume.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
Choose the correct answer of the following question:
The number of solid spheres, each of diameter 6 cm, that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and `1/8` space of the cube remains unfilled. Number of marbles required is
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii?
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
A piece of paper is in the shape of a semi-circular region of radius 10 cm. It is rolled to form a right circular cone. The slant height is ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
A metallic hollow cylindrical pipe has outer and inner radii as 6 cm and 4 cm respectively. Find the volume of the metal used in the pipe of length of 14 cm.
