Advertisements
Advertisements
प्रश्न
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

उत्तर
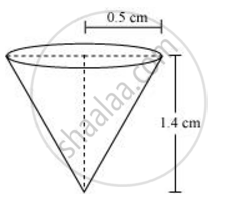
Depth (h) of each conical depression = 1.4 cm
Radius (r) of each conical depression = 0.5 cm
Volume of wood = Volume of cuboid − 4 × Volume of cones
= `"lbh" - 4 xx 1/3pir^2h`
`= 15 xx 10 xx 3.5 - 4 xx 1/3 xx 22/7 xx (1/2)^2 xx 1.4`
= 525 – 1.47
= 523.53 cm3
संबंधित प्रश्न
A cylindrical jar of radius 6cm contains oil. Iron sphere each of radius 1.5cm are immersed in the oil. How many spheres are necessary to raise level of the oil by two centimetress?
The largest sphere is to be curved out of a right circular of radius 7cm and height 14cm. find volume of sphere?
A copper sphere of radius 3cm is melted and recast into a right circular cone of height 3cm.find radius of base of cone?
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
A solid metallic cuboid of dimensions 9 m × 8 m × 2 m is melted and recast into solid cubes of edge 2 m. Find the number of cubes so formed.
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume of water
- displaced out of the cylinder
- left in the cylinder.
A solid piece of iron in the form a cuboid of dimensions (49 cm × 33 cm × 24 cm) is moulded into a solid sphere. The radius of the sphere is ______.
Choose the correct answer of the following question:
The number of solid spheres, each of diameter 6 cm, that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
A metallic hollow cylindrical pipe has outer and inner radii as 6 cm and 4 cm respectively. Find the volume of the metal used in the pipe of length of 14 cm.
