Advertisements
Advertisements
प्रश्न
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

उत्तर
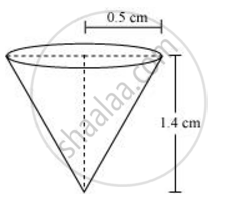
Depth (h) of each conical depression = 1.4 cm
Radius (r) of each conical depression = 0.5 cm
Volume of wood = Volume of cuboid − 4 × Volume of cones
= `"lbh" - 4 xx 1/3pir^2h`
`= 15 xx 10 xx 3.5 - 4 xx 1/3 xx 22/7 xx (1/2)^2 xx 1.4`
= 525 – 1.47
= 523.53 cm3
संबंधित प्रश्न
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
A path 2m wide surrounds a circular pond of diameter 40m. how many cubic meters of gravel are required to grave the path to a depth of 20cm ?
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
A bucket made up of a metal sheet is in form of a frustum of cone of height 16cm with diameters of its lower and upper ends as 16cm and 40cm. find the volume of bucket. Also find cost of bucket if the cost of metal sheet used is Rs 20 per 100 cm2
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
The radii of internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm, respectively. It is melted and recast into a solid cylinder of diameter 14 cm. Find the height of the cylinder.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : curved surface area.
A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.
Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
Given that 1 cu. cm of marble weighs 25 g, the weight of a marble block of 28 cm in width and 5 cm thick, is 112 kg. The length of the block is ______.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A solid is in the shape of a cone standing on a hemisphere with both their diameters being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid. [Use π = 3.14]
