Advertisements
Advertisements
Question
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). Use [π = `22/7`]

Solution
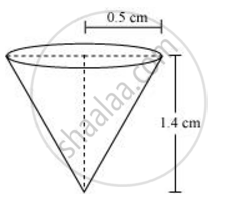
Depth (h) of each conical depression = 1.4 cm
Radius (r) of each conical depression = 0.5 cm
Volume of wood = Volume of cuboid − 4 × Volume of cones
= `"lbh" - 4 xx 1/3pir^2h`
`= 15 xx 10 xx 3.5 - 4 xx 1/3 xx 22/7 xx (1/2)^2 xx 1.4`
= 525 – 1.47
= 523.53 cm3
RELATED QUESTIONS
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
How many spherical bullets each of 5cm in diameter can be cast from a rectangular block of metal 11 dm x 1m x 5 dm?
The volume of a hemisphere is 2425`1/2cm^3`cm. Find its curved surface area?
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use`pi22/7`]
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, then find the volume of wood in the toy.
Choose the correct answer of the following question:
A metallic solid sphere of radius 9 cm is melted to form a solid cylinder of radius 9 cm. The height of the cylinder is
Choose the correct answer of the following question:
If the radius of a sphere becomes 3 times, then its volume will become
Choose the correct answer of the following question:
If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is ______.
How many bags of grain can be stored in a cuboidal granary (8 m × 6 m × 3 m), if each bag occupies a space of 0.64 m3?
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
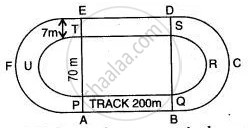
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m calculate the length of the canvas which is 5m wide to make the required tent.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is ______.
500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04m3?
