Advertisements
Advertisements
Question
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
Options
2.1 cm
1.05 cm
1.5 cm
2 cm
Solution
2 . 1 cm
Radius of cone = 2.1 cm
Height of cone = 8.4 cm
Volume of cone`= 1/3 pi"r"^2"h" = 1/3pi (2.1)^2xx8.4`
`"Volume of the sphere" = 4/3 pi"r"^3`
Therefore,
Volume of cone = Volume of sphere
`=> 1/3pixx(2.1)^2xx8.4=4/3pi"r"^3`
⇒ 4.41 × 8.4 = 4r3
⇒ 37.044 = 4r3
`=> "r"^3 = 37.044/4`
= r3 = (2.1)3
APPEARS IN
RELATED QUESTIONS
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed (Use it =`22/7`)
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of \[3\frac{4}{7}\] litre per second. How much time will it take to make the tank half empty?\[\left[ Use \pi = \frac{22}{7} \right]\]
The radii of two cylinders are in the ratio 3 : 5. If their heights are in the ratio 2 : 3, then the ratio of their curved surface areas is
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
The diameter of the base of a cone is 42 cm and its volume is 12936 cm3. Its height is
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
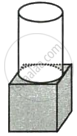
Find the volume and the total surface area of the whole solid. [Take π = 3.14].
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 minutes; if 8 cm standing water is needed?
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
The curved surface area of a right circular cylinder is 176 sq cm and its volume is 1232 cu cm. What is the height of the cylinder?
