Advertisements
Advertisements
Question
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
Solution
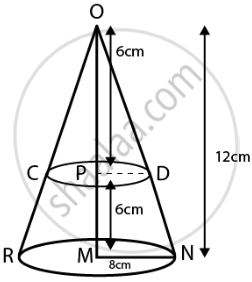
According to the question,
Height of cone = OM = 12 cm
The cone is divided from the mid-point.
Hence, let the mid-point of cone = P
OP = PM = 6 cm
From ΔOPD and ΔOMN
∠POD = ∠POD ...[Common]
∠OPD = ∠OMN ...[Both 90°]
Hence, by the Angle-Angle similarity criterion
We have,
ΔOPD ~ ΔOMN
And
Similar triangles have corresponding sides in equal ratio,
So, we have,
`"PD"/"MN" = "OP"/"OM"`
`"PD"/8 = 6/12`
PD = 4cm ...[MN = 8 cm = radius of base of cone]
For first part i.e. cone
Base radius, r = PD = 4 cm
Height, h = OP = 6 cm
We know that,
Volume of cone for radius r and height h, V = `1/3 π"r"^2"h"`
Volume of first part = `1/3 π(4)^(2)6` = 32π
For second part, i.e. Frustum
Bottom radius, r1 = MN = 8 cm
Top radius, r2 = PD = 4 cm
Height, h = PM = 6 cm
We know that,
Volume of frustum of a cone = `1/3 π"h"("r"_1^2 + "r"_2^2 + "r"_1"r"_2)`, where, h = height, r1 and r2 are radii, (r1 > r2)
Volume of second part = `1/3 π(6)[8^2 + 4^2 + 8(4)]`
= 2π(112)
= 224π
Therefore, we get the ratio,
Volume of first part : Volume of second part = 32π : 224π = 1 : 7
APPEARS IN
RELATED QUESTIONS
Water in a canal 1.5m wide and 6m deep is flowering with a speed of 10km/ hr. how much area will it irrigate in 30 minutes if 8cm of standing water is desired?
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the value of water (i) displaced out of the cylinder (ii) left in the cylinder. (Take π 22/7)
A reservoir in the form of the frustum of a right circular cone contains 44 × 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take: π = 22/7)
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
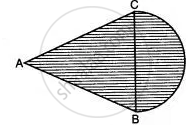
In the equilateral Δ ABC of side 14 cm, side BC is the diameter of a semicircle as shown in the figure below. Find the area of the shaded region. (Take π = 22/7 and √3 = 1.732)
A surahi is the combination of ______.
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that `1/8` space is covered by the mortar. Then the number of bricks used to construct the wall is ______.
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the figure. Calculate the volume of ice cream, provided that its `1/6` part is left unfilled with ice cream.
How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic cm of iron weighs 7.5 g, find the weight of the box.
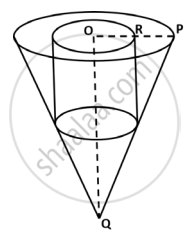
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)