Advertisements
Advertisements
प्रश्न
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
उत्तर
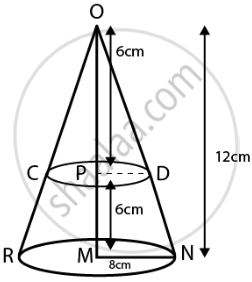
According to the question,
Height of cone = OM = 12 cm
The cone is divided from the mid-point.
Hence, let the mid-point of cone = P
OP = PM = 6 cm
From ΔOPD and ΔOMN
∠POD = ∠POD ...[Common]
∠OPD = ∠OMN ...[Both 90°]
Hence, by the Angle-Angle similarity criterion
We have,
ΔOPD ~ ΔOMN
And
Similar triangles have corresponding sides in equal ratio,
So, we have,
`"PD"/"MN" = "OP"/"OM"`
`"PD"/8 = 6/12`
PD = 4cm ...[MN = 8 cm = radius of base of cone]
For first part i.e. cone
Base radius, r = PD = 4 cm
Height, h = OP = 6 cm
We know that,
Volume of cone for radius r and height h, V = `1/3 π"r"^2"h"`
Volume of first part = `1/3 π(4)^(2)6` = 32π
For second part, i.e. Frustum
Bottom radius, r1 = MN = 8 cm
Top radius, r2 = PD = 4 cm
Height, h = PM = 6 cm
We know that,
Volume of frustum of a cone = `1/3 π"h"("r"_1^2 + "r"_2^2 + "r"_1"r"_2)`, where, h = height, r1 and r2 are radii, (r1 > r2)
Volume of second part = `1/3 π(6)[8^2 + 4^2 + 8(4)]`
= 2π(112)
= 224π
Therefore, we get the ratio,
Volume of first part : Volume of second part = 32π : 224π = 1 : 7
APPEARS IN
संबंधित प्रश्न
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass. [Use π = 3.14]
A hollow sphere of internal and external diameter 4cm and 8cm is melted into a cone of base diameter 8cm. Calculate height of cone?
A cylindrical vessel of diameter 14cm and height 42cm is fixed symmetrically inside a similar vessel of diameter 16cm and height 42 . cm The total space between two vessels is filled with cork dust for heat insulation purpose. How many cubic cms of cork dust will be
required?
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7`litres per sec.
How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
The area of the base of a rectangular tank is 6500 cm2 and the volume of water contained in it is 2.6 m3. The depth of water in the tank is
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
A piece of paper is in the shape of a semi-circular region of radius 10 cm. It is rolled to form a right circular cone. The slant height is ______.
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
A metallic hollow cylindrical pipe has outer and inner radii as 6 cm and 4 cm respectively. Find the volume of the metal used in the pipe of length of 14 cm.
From a soild cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid.
