Advertisements
Advertisements
प्रश्न
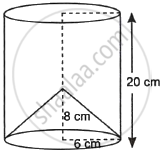
From a soild cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid.
उत्तर
Given, Height of cylinder h1 = 20 cm
Radius of cylinder = `12/2` = 6 cm.
Height of the cone (h2) = 8 cm.
Radius of the cone r = 6 cm.
Total surface area of remaining solid = Curved surface area of cylinder + Curved surface area of cone + Area of the top face of the cylinder
Slant height of the cone (l) = `sqrt("h"_2^2 + "r"^2)`
= `sqrt(8^2 + 6^2)`
= `sqrt(64 + 36)`
= 10 cm.
∴ Curved surface area of cone = πrl
= `22/7 xx 6 xx 10`
= `1320/7` cm2
Curved surface area of cylinder = 2πrh
= `2 xx 22/7 xx 6 xx 20`
= `5280/7` cm2
Area of the top face of the cylinder = πr2
= `22/7 xx 6 xx 6`
= `792/7` cm2
∴ Total surface area of the remaining solid
= `1320/7 + 5280/7 + 792/7`
= `7392/7`
= 1056 cm2
APPEARS IN
संबंधित प्रश्न
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub (Take π = 22/7)
A boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
A toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, then find the height of the toy.
A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 2.1 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the cylinder is 5 cm and its height is 9.8 cm, find the volume of the water left in the tub.
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
A hemispherical bowl of internal radius 9 cm is full of water. This water is to be filled in cylindrical bottles of diameter 3 cm and height 4 cm. Find the number of bottles needed in which the water can be filled.
How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9 cm × 11cm × 12cm?
Read the following passage and answer the questions given below.
|
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.