Advertisements
Advertisements
प्रश्न
From a soild cylinder of height 20 cm and diameter 12 cm, a conical cavity of height 8 cm and radius 6 cm is hallowed out. Find the total surface area of the remaining solid.
उत्तर
Given, Height of cylinder h1 = 20 cm
Radius of cylinder = `12/2` = 6 cm.
Height of the cone (h2) = 8 cm.
Radius of the cone r = 6 cm.
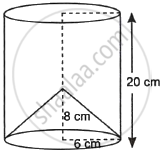
Total surface area of remaining solid = Curved surface area of cylinder + Curved surface area of cone + Area of the top face of the cylinder
Slant height of the cone (l) = `sqrt("h"_2^2 + "r"^2)`
= `sqrt(8^2 + 6^2)`
= `sqrt(64 + 36)`
= 10 cm.
∴ Curved surface area of cone = πrl
= `22/7 xx 6 xx 10`
= `1320/7` cm2
Curved surface area of cylinder = 2πrh
= `2 xx 22/7 xx 6 xx 20`
= `5280/7` cm2
Area of the top face of the cylinder = πr2
= `22/7 xx 6 xx 6`
= `792/7` cm2
∴ Total surface area of the remaining solid
= `1320/7 + 5280/7 + 792/7`
= `7392/7`
= 1056 cm2
APPEARS IN
संबंधित प्रश्न
How many coins 1.75cm in diameter and 2mm thick must be melted to form a cuboid 11cm x 10cm x 75cm___?
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
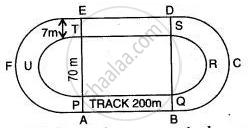
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
Read the following passage and answer the questions given below.
|
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.