Advertisements
Advertisements
प्रश्न
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
उत्तर
Let us first calculate the volume of barrel of pen that is of cylindrical shape
Consider barrel,
Since 1 cm = 10 mm
Base diameter = 5 mm = 0.5 cm
Base radius, r = 0.25 cm
Height, h = 7 cm
We know that,
Volume of a cylinder = πr2h
Volume of barrel = π(0.25)27
Volume of barrel = `22/7 xx 0.25 xx 0.25 xx 7` = 1.375 cm3
Hence, according to the question,
1.375 cm3 of ink can write 3300 words
No of words that can be written by 1 cm3 of ink = `3300/1.375` = 2400 words
1/5th of a liter = 0.2L
We know that,
1L = 1000 cm3
0.2L = 200 cm3
So, no of words that can be written by 200 cm3 = 2400(200) = 480000 words
Therefore, 1/5th of a liter ink can write 480000 words.
APPEARS IN
संबंधित प्रश्न
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [use `pi = 22/7`]
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
A rectangular tank 15m long and 11m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5m. Find least height of tank that will serve purpose .
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7`litres per sec.
How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
A metallic cone of base radius 2.1 cm and height 8.4 cm is melted and moulded into a sphere. The radius of the sphere is
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that `1/8` space of the cube remains unfilled. Then the number of marbles that the cube can accomodate is ______.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
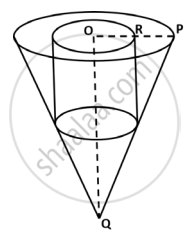
A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood. (Use, `pi = 22/7`)