Advertisements
Advertisements
Question
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
Solution
Let us first calculate the volume of barrel of pen that is of cylindrical shape
Consider barrel,
Since 1 cm = 10 mm
Base diameter = 5 mm = 0.5 cm
Base radius, r = 0.25 cm
Height, h = 7 cm
We know that,
Volume of a cylinder = πr2h
Volume of barrel = π(0.25)27
Volume of barrel = `22/7 xx 0.25 xx 0.25 xx 7` = 1.375 cm3
Hence, according to the question,
1.375 cm3 of ink can write 3300 words
No of words that can be written by 1 cm3 of ink = `3300/1.375` = 2400 words
1/5th of a liter = 0.2L
We know that,
1L = 1000 cm3
0.2L = 200 cm3
So, no of words that can be written by 200 cm3 = 2400(200) = 480000 words
Therefore, 1/5th of a liter ink can write 480000 words.
APPEARS IN
RELATED QUESTIONS
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
The diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross-section. If the length of the wire is 108 m, find its diameter.
A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.
A hollow metallic sphere with external diameter 8 cm and internal diameter 4 cm is melted and moulded into a cone of base radius 8 cm. The height of the cone is
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 minutes; if 8 cm standing water is needed?
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
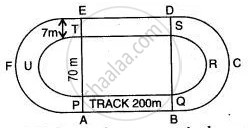
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is `4/3 pia^3`.
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
