Advertisements
Advertisements
Question
The diameter of a copper sphere is 18 cm. It is melted and drawn into a long wire of uniform cross-section. If the length of the wire is 108 m, find its diameter.
Solution
Diameter of sphere = 18 cm
Radius of the sphere = 9 cm
Volume of sphere`=4/3 pir^3 = 4/3pixx9xx9xx9 "cm"^3`
Length of wire = 108 m = 10800 cm
Let radius of the wire be r cm.
Volume of the wire` = pir^2l = pixxr^2xx10800 "cm"^3`
The Volume of the sphere and the wire are the same.
Therefore,
`pixxr^2xx10800 = 4/3pixx9xx9xx9`
`rArr r^2 =(4xx9xx9xx9)/(3xx10800) = (4xx9xx9)/(3xx4xx3) =0.9 `
`rArr r^2 =sqrt(0.09) = 0.3 "cm"`
Thus, d=2r =2 ×0.3 cm = 0.6 cm
The diameter of the wire is 0.6 cm.
APPEARS IN
RELATED QUESTIONS
What length of a solid cylinder 2cm in diameter must be taken to recast into a hollow
cylinder of length 16cm, external diameter 20cm and thickness 2.5mm?
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
A solid toy is in the form of a hemisphere surmounted by a right circular cone. height of the cone is 2 cm and the diameter of the base is 4 cm. If a right circular cylinder circumscribes the toy, find how much more space it will cover.
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.
How many bricks, each measuring (25 cm × 11.25 cm × 6 cm), will be required to construct a wall (8 m × 6 m × 22.5 cm)?
The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as `22/7`, the capacity of bowl in cm³ is ______.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder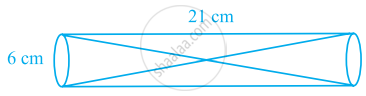
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
