Advertisements
Advertisements
Question
A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains `41 19/21 m^3` of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
Solution
Let total height of the building = Internal diameter of the dome = 2r m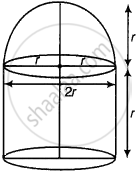
∴ Radius of building (or dome) = `(2r)/2` = r m
Height of cylinder = 2r – r = r m
∴ Volume of the cylinder = πr2(r) = πr3m3
And volume of hemispherical dome cylinder = `2/3 pir^3m^3`
∴ Total volume of the building
= Volume of the cylinder + Volume of hemispherical dome
= `(pir^3 + 2/3 pir^3)m^3`
= `5/3 pir^3m^3`
According to the question,
Volume of the building = Volume of the air
⇒ `5/3 pir^3 = 41 19/21`
⇒ `5/3 pir^3 = 880/21`
⇒ r3 = `(880 xx 7 xx 3)/(21 xx 22 xx 5)`
= `(40 xx 21)/(21 xx 5)`
= 8
⇒ r3 = 8
⇒ r = 2
∴ Height of the building = 2r
= 2 × 2
= 4 m
APPEARS IN
RELATED QUESTIONS
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
The diameters of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder.
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of \[3\frac{4}{7}\] litre per second. How much time will it take to make the tank half empty?\[\left[ Use \pi = \frac{22}{7} \right]\]
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm3, then find the radius of the base of the cylinder.
Match the following columns:
| Column I | Column II |
| (a) A solid metallic sphere of radius 8 cm is melted and the material is used to make solid right cones with height 4 cm and base radius of 8 cm. How many cones are formed? | (p) 18 |
| (b) A 20-m-deep well with diameter 14 m is dug up and the earth from digging is evenly spread out to form a platform 44 m by 14 m. The height of the platform is ...........m. |
(q) 8 |
| (c) A sphere of radius 6 cm is melted and recast in the shape of a cylinder of radius 4 cm. Then, the height of the cylinder is ......... cm. |
(r) 16 : 9 |
| (d) The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ....... . |
(s) 5 |
The volumes of two spheres are in the ratio 27 : 8. The ratio of their curved surface is ______.
A solid iron cuboidal block of dimensions 4.4 m × 2.6 m × 1 m is recast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
