Advertisements
Advertisements
Question
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Solution
We have
Radius of the cylincler = `12/2` = 6 cm
Height of the cylinder = 15 cm
∴ Volume of the cy linder = πr2h
= π × 62 × 15
= 540π cm3
Radius of the ice-cream cone = 3 cm
Height of the ice-cream cone = 12 cm
∴ Volume of the conical part of ice-cream cone = `1/3 pir^2h`
Volume of the conical part of ice-cream cone = `1/3 xx pi xx 3^2 xx 12 cm^3`
Volume of the conical part of ice-cream cone = 36π cm3
Volume of the hemispherical top of the ice-cream = `2/3pir^3`
= `2/3 xx pi xx 3^3`
= 18π cm3
Total volume of the ice-cream cone
= (36π + 18π) cm3
= 54π cm3
∴ Number of ice-cream cone
= `"Volume of the cylinder"/"Total volume of ice-cream"`
= `(540pi)/(54pi)`
= 10
APPEARS IN
RELATED QUESTIONS
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
The diameters of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder.
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. (Use π = 22/7).
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be 1/125 of the volume of the original cone, determine at what height above the base the section is made.
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7`litres per sec.
How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
If the volumes of two cones are in the ratio of 1:4 and their diameters are in the ratio of 4:5, then find the ratio of their heights.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
A mason constructs a wall of dimensions (270 cm × 300 cm × 350 cm) with bricks, each of size (22.5 cm × 11.25 cm × 8.75 cm) and it is assumed that `1/8` space is covered by the mortar. Number of bricks used to construct the wall is ______.
Rainfall in an area is 5 cm. The volume of the water that falls on 2 hectares of land is
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
A solid rectangular block of dimensions 4.4 m, 2.6 m and 1 m is cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
In a swimming pool measuring 90 m × 40 m, 150 men take a dip. If the average displacement of water by a man is 8 m3, then rise in water level is ______.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder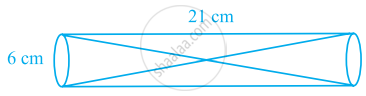
The rain water from a roof of dimensions 22 m × 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
A solid is in the shape of a right-circular cone surmounted on a hemisphere, the radius of each of them being 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
A student was asked to make a model shaped like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.
An ice-cream filled cone having radius 5 cm and height 10 cm is as shown in the figure. Find the volume of the ice-cream in 7 such cones.

