Advertisements
Advertisements
Question
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
Solution
Given that inner radius of a well (a)= 4am
Depth of a well (h) = 14m
Volume of a cylinder = πr2h
V1 = π(4)2 x 14cm3 .................(1)
Given well is spread evenly to form an embankment
Width of an embankment = 3m
Outer radii of a well(R) = 4 + 3 = 7m.
Volumeof a hollow cylinder `=pi(R^2-r^2)xxhm^3`
`V_2=pi(7^2-4^2)xxhm^3` ............(2)
Equating (1) and (2)
V1 = V2
⇒ `pi(4)^2xx14=pi(49-16)xxh`
⇒ `h=(pi(4)^2xx14)/(pipi(33))`
h = 6.78m
APPEARS IN
RELATED QUESTIONS
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass. [Use π = 3.14]
500 persons have to dip in a rectangular tank which is 80m long and 50m broad. What is the rise in the level of water in the tank, if the average displacement of water by a person is 0.04m3 .
A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?
The sum of the radius of the base and the height of a solid cylinder is 37 metres. If the total surface area of the cylinder be 1628 sq metres, then find its volume.
A cube of side 6 cm is cut into a number of cubes, each of side 2 cm. The number of cubes formed is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m calculate the length of the canvas which is 5m wide to make the required tent.
The radius of a wire is decreased to one third. If volume remains the same, the length will become ______.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder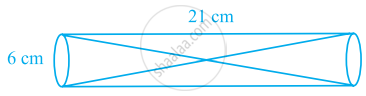
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
