Advertisements
Advertisements
Questions
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
Solution
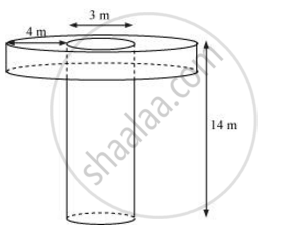
The shape of the well will be cylindrical.
Depth (h1) of well = 14 m
Radius (r1) of the circular end of well = 3/2 m
Width of embankment = 4 m
From the figure, it can be observed that our embankment will be in a cylindrical shape having outer radius (r2) as 4 + 3/2 =11/2 m and inner radius (r1) as 3/2 m
Let the height of embankment be h2.
Volume of soil dug from well = Volume of earth used to form embankment
`pixxr_1^2xxh_1 = pixx(r_2^2-r_1^2)xxh_2`
`pixx(3/2)^2xx 14 =pixx[(11/2)^2-(3/2)^2]xxh`
`9/4xx14 = 112/4 xx h`
h = 9/8 = 1.125 m
Therefore, the height of the embankment will be 1.125 m.
RELATED QUESTIONS
A solid is in the shape of a frustum of a cone. The diameter of two circular ends are 60cm and 36cm and height is 9cm. find area of its whole surface and volume?
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/hr. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired ?
Water is flowing at the rate of 6 km/hr through a pipe of diameter 14 cm into a rectangular tank which is 60 m long and 22 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/hr. How much area will it irrigate in 10 minutes if 8 cm of standing water is needed for irrigation?
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The radius of the base of a cone is 5 cm and its height is 12 cm. Its curved surface area is
The total surface area of a hemisphere of radius 7 cm is
Assertion (A)
The curved surface area of a cone of base radius 3 cm and height 4 cm is 15π cm2.\
Reason (R)
Volume of a cone = πr2h
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
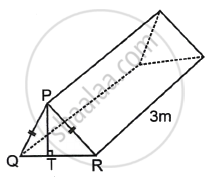
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent