Advertisements
Advertisements
Question
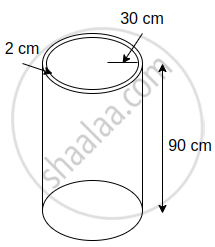
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
Solution
Given,
For the cylindrical tube:
height (h) = 90 cm
Outer Radius (R) = 30 cm,
Thickness = 2 cm
For the plastic spherical ball:
radius (r) = 1 cm
Inner radius of tube (r) = Outer radius − Thickness of tube
= 30 − 2
= 28 cm
Volume of plastic required for the tube = Outer volume of tube − Inner volume of hollow tube
= πR2h − πr2h
= πh(R2 − r2)
= π × 90 (302 − 282)
= π × 90 (900 − 784)
= π × 90 × 116 cm3
Volume of one plastic ball = `4/3πr_1^3`
= `4/3π × 1^3`
= `4/3π` cm3
`"Number of balls to be melted" = "Volume of plastic required for the tube"/"Volume of one plastic ball"`
= `(cancelπ × 90 × 116)/(4/3 cancelπ)`
= `(90 × 116 × 3)/(4)`
= 90 × 29 × 3
= 7830
Thus, the number of plastic balls melted to make the tube are 7830.
APPEARS IN
RELATED QUESTIONS
In Fig. 5, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre `( "Use "pi=22/7)`

Water is flowing at the rate of 2.52 km/h through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3.15 m, find the internal diameter of the pipe.
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
A solid sphere of diameter 6 cm is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
A hemispherical bowl of internal radius 9 cm is full of liquid . The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm . How many bottles are needed to empty the bowl ?
Find the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
A golf ball has diameter equal to 4.2 cm. Its surface has 200 dimples each of radius 2 mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.
If the volumes of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5, then write the ratio of their weights.
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
The radius of the base and the height of a solid right circular cylinder are in the ratio 2 : 3 and its volume is 1617 cm3. Find the total surface area of the cylinder.
Arrange the given objects according to their volume
A cube whose edge is 20 cm long, has circles on each of its faces painted black. What is the total area of the unpainted surface of the cube if the circles are of the largest possible areas?
A bicycle wheel makes 500 revolutions in moving 1 km. Find the diameter of the wheel.
A boy is cycling such that the wheels of the cycle are making 140 revolutions per hour. If the diameter of the wheel is 60 cm, calculate the speed in km/h with which the boy is cycling.
The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
