Advertisements
Advertisements
प्रश्न
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
उत्तर
Given,
For the cylindrical tube:
height (h) = 90 cm
Outer Radius (R) = 30 cm,
Thickness = 2 cm
For the plastic spherical ball:
radius (r) = 1 cm
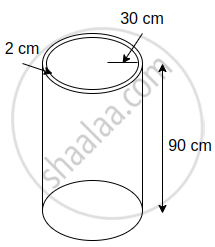
Inner radius of tube (r) = Outer radius − Thickness of tube
= 30 − 2
= 28 cm
Volume of plastic required for the tube = Outer volume of tube − Inner volume of hollow tube
= πR2h − πr2h
= πh(R2 − r2)
= π × 90 (302 − 282)
= π × 90 (900 − 784)
= π × 90 × 116 cm3
Volume of one plastic ball = `4/3πr_1^3`
= `4/3π × 1^3`
= `4/3π` cm3
`"Number of balls to be melted" = "Volume of plastic required for the tube"/"Volume of one plastic ball"`
= `(cancelπ × 90 × 116)/(4/3 cancelπ)`
= `(90 × 116 × 3)/(4)`
= 90 × 29 × 3
= 7830
Thus, the number of plastic balls melted to make the tube are 7830.
APPEARS IN
संबंधित प्रश्न
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
Radius of a sphere is 14 cm. Find the surface area of the sphere.
A tank of cylindrical shape has radius 2.8 m and its height 3.5 m. Complete the activity to find how many litres of water the tank will contain.
Capacity of water tank = Volume of cylindrical tank
= πr2h
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use \[\pi = \frac{22}{7}\]]
A pen stand made of wood is in the shape of a cuboid with four conical depression and a cubical depression to hold the pens and pins , respectively . The dimension of the cuboid are \[10 cm \times 5 cm \times 4 cm\].
The radius of each of the conical depression is 0.5 cm and the depth is 2.1 cm . The edge of the cubical depression is 3 cm . Find the volume of the wood in the entire stand.
A sphere of diameter 5 cm is dropped into a cylindrical vessel partly filled with water. The diameter of the base of the vessel is 10 cm. If the sphere is completely submerged, by how much will the level of water rise?
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm are cut off. Find the volume of the remaining solid.
Two cubes have their volumes in the ratio 1 : 27. What is the ratio of their surface areas?
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii ?
From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid. Also, find the total surface area of the remaining solid.
A farmer connects a pipe of internal diameter 25 cm from a canal into a cylindrical tank in his field, which is 12 m in diameter and 2.5 m deep. If water flows through the pipe at the rate of 3.6 km/hr, then in how much time will the tank be filled? Also, find the cost of water if the canal department charges at the rate of ₹ 0.07 per m3.
66 cubic cm of silver is drawn into a wire 1 mm in diameter. Calculate the length of the wire in metres.
The curved surface area of a sphere is 5544 cm2. Find its volume.
A solid metallic sphere of diameter 8 cm is melted and drawn into a cylindrical wire of uniform width. If the length of the wire is 12 m, then find its width.
If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, then find its capacity and total surface area.
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
The area of the base of a right circular cone is 154 cm2 and its height is 14 cm. Its curved surface area is
If the radii of the ends of a bucket are 5 cm and 15 cm and it is 24 cm high, then its surface area is
The radius of the base and the height of a solid right circular cylinder are in the ratio 2 : 3 and its volume is 1617 cm3. Find the total surface area of the cylinder.
The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
