Advertisements
Advertisements
Question
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
Solution
Radius of the sphere `=42/2 = 21 "cm"`
volume of sphere`=4/3pi"r"^3`
`=(4/3pixx21xx21xx21) "cm"^3`
Radius of the wire `=2.8/2 = 1.4 "cm" `
Let the length of the wire be h cm. then,
Volume of the wire= πr2h
`=(pixx14/10xx14/10xx"h")"cm^3"`
Therefore
`4/3 pixx21xx21xx21=pixx14/10xx14/10`
`=>12348=(49/25)xx"h"`
`=> "h" = 6300 "cm"`
`=> "h" =(6300/100) "m"`
⇒ h = 63 m
Hence, the length of the wire is 63 m.
APPEARS IN
RELATED QUESTIONS
In Fig. 5, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre `( "Use "pi=22/7)`

A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
A cylindrical container is filled with ice-cream, whose diameter is 12 cm and height is 15 cm. the whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water . Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm .
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
Water is flowing at the rate of 6 km/hr through a pipe of diameter 14 cm into a rectangular tank which is 60 m long and 22 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
Choose the correct answer of the following question:
A solid is hemispherical at the bottom and conical (of same radius) above it. If the surface areas of the two parts are equal, then the ratio of its radius and the slant height of the conical part is
The shape of a gilli, in the gilli-danda game (see Fig.), is a combination of ______.

What is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
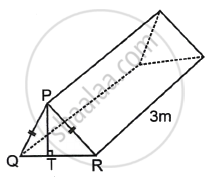
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent