Advertisements
Advertisements
Question
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent
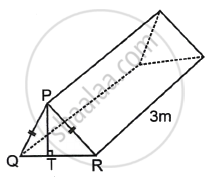
Solution
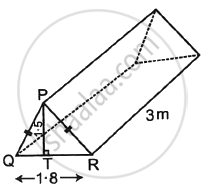
Given: QR = 1.8 m, PT = 1.5 m, PQ = PR.
Since, PQ = PR
So, ΔPQR is an isosceles triangle.
So, PT bisects QR.
∴ QT = `1.8/2` = 0.9
i. tan Q = `"Perpendicular"/"Base"`
tan Q = `(1.5)/(0.9)`
tan Q = 1.6666666667
⇒ Q = 59.036°
Hence, ∠PQR = 59.036°.
ii. Volume of the tent,
V = `1/2` LWH
Here, L = 3 m, W = 1.8 m and H = 1.5 m
∴ V = `1/2 xx 3 xx 1.8 xx 1.5` = 4.05 m3
As a result, the volume of the tent is 4.05 m3.
APPEARS IN
RELATED QUESTIONS
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/12 cm, find the length of the wire.
A right angled triangle whose sides are 3 cm, 4 cm and 5 cm is revolved about the sides containing the right angle in two days. Find the difference in columes of the two cones so formed. Also, find their curved surfaces.
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm. find the number of lead spheres dropped in the water.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 km2. Find the height of the mountain.
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
Choose the correct answer of the following question:
A solid is hemispherical at the bottom and conical (of same radius) above it. If the surface areas of the two parts are equal, then the ratio of its radius and the slant height of the conical part is
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
Find the surface area of a sphere of radius 3.5 cm.

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?

In Figure 3, a decorative block is shown which is made of two solids, a cube, and a hemisphere. The base of the block is a cube with an edge 6 cm and the hemisphere fixed on the top has a diameter of 4⋅2 cm. Find
(a) the total surface area of the block.
(b) the volume of the block formed. `("Take" pi = 22/7)`
Arrange the given objects according to their volume
The slant height of a bucket is 26 cm. The diameter of upper and lower circular ends are 36 cm and 16 cm. then height of bucket is ______.
A surahi is the combination of ______.
The shape of a gilli, in the gilli-danda game (see Fig.), is a combination of ______.

A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter ______.
The internal and external radii of a spherical shell are 3cm and 5cm respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. Also find the total surface area of the cylinder. (Take `pi = 22/7`)
