Advertisements
Advertisements
प्रश्न
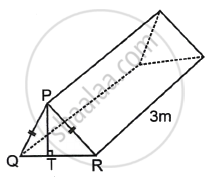
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent
उत्तर
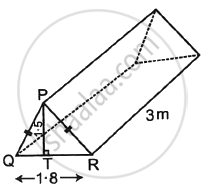
Given: QR = 1.8 m, PT = 1.5 m, PQ = PR.
Since, PQ = PR
So, ΔPQR is an isosceles triangle.
So, PT bisects QR.
∴ QT =
i. tan Q =
tan Q =
tan Q = 1.6666666667
⇒ Q = 59.036°
Hence, ∠PQR = 59.036°.
ii. Volume of the tent,
V =
Here, L = 3 m, W = 1.8 m and H = 1.5 m
∴ V =
As a result, the volume of the tent is 4.05 m3.
APPEARS IN
संबंधित प्रश्न
A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond ?
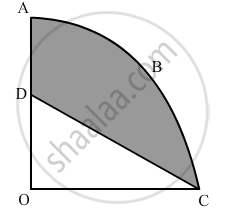
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?
Find the volume of a sphere of diameter 6 cm.
The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of Rs. 10 per sq.m.
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m × 16 m × 11 m.
A hollow sphere of internal and external diameters 4 and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4, what is the ratio of their volumes?
A solid metallic spherical ball of diameter 6 cm is melted and recast into a cone with diameter of the base as 12 cm. The height of the cone is
The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 km2. Find the height of the mountain.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
Choose the correct answer of the following question:
The radii of the circular ends of a bucket of height 40 cm are 24 cm and 15 cm. The slant height (in cm) of the bucket is
The total surface area of a cube is 864 cm2. Its volume is
Assertion (A)
The curved surface area of a cone of base radius 3 cm and height 4 cm is 15π cm2.\
Reason (R)
Volume of a cone = πr2h
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The radius of the base and the height of a solid right circular cylinder are in the ratio 2 : 3 and its volume is 1617 cm3. Find the total surface area of the cylinder.
A circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square?
Ratio of area of a circle to the area of a square whose side equals radius of circle is 1 : π.
