Advertisements
Advertisements
प्रश्न
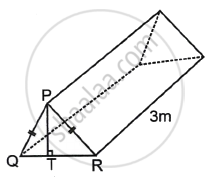
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent
उत्तर
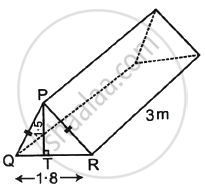
Given: QR = 1.8 m, PT = 1.5 m, PQ = PR.
Since, PQ = PR
So, ΔPQR is an isosceles triangle.
So, PT bisects QR.
∴ QT = `1.8/2` = 0.9
i. tan Q = `"Perpendicular"/"Base"`
tan Q = `(1.5)/(0.9)`
tan Q = 1.6666666667
⇒ Q = 59.036°
Hence, ∠PQR = 59.036°.
ii. Volume of the tent,
V = `1/2` LWH
Here, L = 3 m, W = 1.8 m and H = 1.5 m
∴ V = `1/2 xx 3 xx 1.8 xx 1.5` = 4.05 m3
As a result, the volume of the tent is 4.05 m3.
APPEARS IN
संबंधित प्रश्न
Water is flowing at the rate of 2.52 km/h through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3.15 m, find the internal diameter of the pipe.
To fill a swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool.
A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
The dimensions of a solid iron cuboid are 4·4 m × 2·6 m × 1·0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
A tent is in the form of a cylinder of diameter 20 m and height 2.5 m, surmounted by a cone of equal base and height 7.5 m. Find the capacity of the tent and the cost of the canvas at Rs 100 per square metre.
Radius of a sphere is 14 cm. Find the surface area of the sphere.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
A hemispherical tank, full of water, is emptied by a pipe at the rate of `25/7` litres per second. How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m?
A farmer connects a pipe of internal diameter 25 cm from a canal into a cylindrical tank in his field, which is 12 m in diameter and 2.5 m deep. If water flows through the pipe at the rate of 3.6 km/hr, then in how much time will the tank be filled? Also, find the cost of water if the canal department charges at the rate of ₹ 0.07 per m3.
A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.
Choose the correct answer of the following question:
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
Find the number of solid spheres, each of diameter 6 cm, that could be moulded to form a solid metallic cylinder of height 45 cm and diameter 4 cm.

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter ______.
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
