Advertisements
Advertisements
प्रश्न
Given: O is the centre of the circle, AB is a diameter, OA = AP, O – A – P, PC is a tangent through C. A tangent through point A intersects PC in E and BC in D.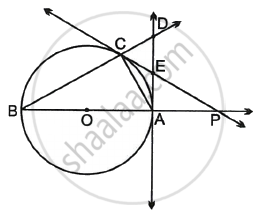
To prove: ΔCED is an equilateral triangle.
उत्तर
Given: OA = AP, PC is a tangent at C, AD is tangent at A.
To prove: ΔCED is an equilateral angle.
Construction: Join OC and OE.
Proof: AD is a tangent to the circle at A.
∴ ∠ACP = ∠ABC ......(i) [Alternate segment theorem]
Since the measure of the angle an arc subtends at a point on a circle is half that of the angle the arc subtends at its centre
∴ ∠ABC = `1/2` ∠AOC ......(ii)
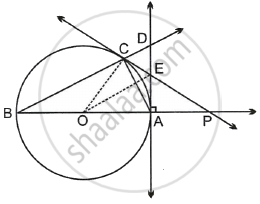
In ΔAOE and ΔCOE
OA ≅ OC ......[Radii of circle]
OE ≅ OE ......[Common side]
AE ≅ CE ......[Tangents to the circle from point E]
∴ By SSS criterion of congruence,
ΔAOE ≅ ΔCOE
∴ ∠AOE = ∠COE ......[C.A.C.T]
or ∠AOE = ∠COE = `1/2` ∠AOC ......(iii)
From equations (ii) and (iii),
∠ABC = ∠AOE ......(iv)
Now, in ΔOEP
AE is the bisector of ∠OEP
∴ `(OA)/(AP) = (OE)/(EP)`
⇒ OE = EP ......[∵ OA = AP, Given]
∴ ∠AOE = ∠APE .....(v) [Angles opposite to equal sides]
or ∠ABC = ∠APE .....(vi) [Using equation (iv)]
From the figure,
∠DCE = 90° – ∠ACP .....(vii)
∠CDE = 90° – ∠ABC ......(viii)
∠AEP = ∠CED = 90° – ∠APE ......(ix) [∠AEP = ∠CED; Vertically opposite angles]
From equations (vii), (viii) and (ix)
∠DCE = ∠CDE = ∠CED
or DE = CE = CD ......[Sides opposite to equal angles]
Hence ΔCED is an equilateral triangle.
Hence Proved.
APPEARS IN
संबंधित प्रश्न
Draw the tangents to the circle from the point L with radius 2.7 cm. Point ‘L’ is at a distance 6.9 cm from the centre ‘M’.
Draw tangents to the circle with center ‘C’ and radius 3.6 cm, from a point B at a distance of 7.2 cm from the center of the circle.
Construct tangents to the circle from the point B, having radius 3.2 cm and centre 'C'. Point B is at a distance 7.6 cm from the centre.
Draw a circle with centre P and radius 3.4 cm. Take point Q at a distance 5.5 cm from the centre. Construct tangents to the circle from point Q.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Draw a circle of diameter 6.4 cm. Take a point R at a distance equal to its diameter from the centre. Draw tangents from point R.
Draw a circle of radius 3.4 cm and centre E. Take a point F on the circle. Take another point A such that E-F-A and FA = 4.1 cm. Draw tangents to the circle from point A.
Draw a circle with centre P and radius 2.1 cm. Take point Q at a distance 5.2 cm from the centre. Draw tangents to the circle from point Q. Measure and write the length of a tangent segment.
Draw a circle with radius 4.2 cm. Construct tangents to the circle from a point at a distance of 7 cm from the centre.
Construct tangents to the circle from the point B, having radius 3.2 cm and centre 'C'. Point B is at a distance 7.2 cm from the centre.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Draw a circle with a radius of 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Draw a circle with radius 4 cm and construct two tangents to a circle such that when those two tangents intersect each other outside the circle they make an angle of 60° with each other
Draw a circle with center O and radius 3 cm. Take point P outside the circle such that d (O, P) = 4.5 cm. Draw tangents to the circle from point P.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
