Advertisements
Advertisements
प्रश्न
Draw tangents to the circle with center ‘C’ and radius 3.6 cm, from a point B at a distance of 7.2 cm from the center of the circle.
उत्तर
Construction:

Steps of Construction:
- Construct a circle with centre C and radius 3.6 cm. Take point B such that CB = 7.2 cm.
- Obtain Midpoint M of seg CB. Draw a circle with centre M and radius MB.
- Let A and D be the points of intersection of these two circles. Draw lines BA and BD which are the required tangents.

APPEARS IN
संबंधित प्रश्न
Draw the tangents to the circle from the point L with radius 2.7 cm. Point ‘L’ is at a distance 6.9 cm from the centre ‘M’.
Construct tangents to the circle from the point B, having radius 3.2 cm and centre 'C'. Point B is at a distance 7.6 cm from the centre.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Draw a circle of diameter 6.4 cm. Take a point R at a distance equal to its diameter from the centre. Draw tangents from point R.
Draw a circle of radius 3.4 cm and centre E. Take a point F on the circle. Take another point A such that E-F-A and FA = 4.1 cm. Draw tangents to the circle from point A.
Draw a circle with centre P and radius 2.1 cm. Take point Q at a distance 5.2 cm from the centre. Draw tangents to the circle from point Q. Measure and write the length of a tangent segment.
Draw a circle with radius 4.2 cm. Construct tangents to the circle from a point at a distance of 7 cm from the centre.
Construct tangents to the circle from the point B, having radius 3.2 cm and centre 'C'. Point B is at a distance 7.2 cm from the centre.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Draw a circle with a radius of 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Draw a circle with radius 4 cm and construct two tangents to a circle such that when those two tangents intersect each other outside the circle they make an angle of 60° with each other
Given: O is the centre of the circle, AB is a diameter, OA = AP, O – A – P, PC is a tangent through C. A tangent through point A intersects PC in E and BC in D.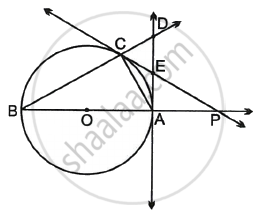
To prove: ΔCED is an equilateral triangle.
