Advertisements
Advertisements
प्रश्न
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
उत्तर
Steps of Construction:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.
∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°
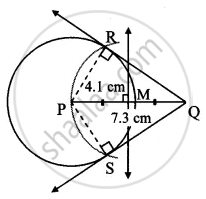
∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.

संबंधित प्रश्न
Draw the tangents to the circle from the point L with radius 2.7 cm. Point ‘L’ is at a distance 6.9 cm from the centre ‘M’.
Draw tangents to the circle with center ‘C’ and radius 3.6 cm, from a point B at a distance of 7.2 cm from the center of the circle.
Construct tangents to the circle from the point B, having radius 3.2 cm and centre 'C'. Point B is at a distance 7.6 cm from the centre.
Draw a circle of diameter 6.4 cm. Take a point R at a distance equal to its diameter from the centre. Draw tangents from point R.
Draw a circle of radius 3.4 cm and centre E. Take a point F on the circle. Take another point A such that E-F-A and FA = 4.1 cm. Draw tangents to the circle from point A.
Draw a circle with centre P and radius 2.1 cm. Take point Q at a distance 5.2 cm from the centre. Draw tangents to the circle from point Q. Measure and write the length of a tangent segment.
Draw a circle with radius 4.2 cm. Construct tangents to the circle from a point at a distance of 7 cm from the centre.
Draw the tangents to the circle from the point L with radius 3 cm. Point ‘L’ is at a distance 8 cm from the centre ‘M’.
Construct tangents to the circle from the point B, having radius 3.2 cm and centre 'C'. Point B is at a distance 7.2 cm from the centre.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Draw a circle with radius 4 cm and construct two tangents to a circle such that when those two tangents intersect each other outside the circle they make an angle of 60° with each other
Draw a circle with center O and radius 3 cm. Take point P outside the circle such that d (O, P) = 4.5 cm. Draw tangents to the circle from point P.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Given: O is the centre of the circle, AB is a diameter, OA = AP, O – A – P, PC is a tangent through C. A tangent through point A intersects PC in E and BC in D.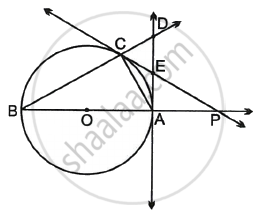
To prove: ΔCED is an equilateral triangle.
