Advertisements
Advertisements
प्रश्न
A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.
उत्तर
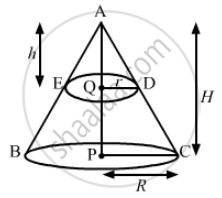
We have,
Radius of solid cone, R = CP = 10 cm,
Let the height of the solid cone be, AP = H,
the radius of the smaller cone, QD = r and
the height of the smaller cone be, AQ = h.
Also, `"AQ"= "AP"/2 "i.e" "h"="H"/2 or "H = 2h" .......(i)`
Now, in Δ AQD and Δ APC
∠QAD = ∠PAC (Common angle)
∠AQD = ∠APC = 90°
So, by AA criteria
ΔAQD ˜ ΔAPC
`⇒ ("AQ")/("AP") = ("QD")`
`rArr "h"/"H" = "r"/"R"`
`rArr "h"/"2h" = r/"R"` [Using (i)]
`rArr 1/2 = "r"/"R"`
`rArr "R" = 2"r"` ..............(ii)
As,
Volume of smaller cone `= 1/3 pi"r"^2"h" `
And,
Volume of solid cone `= 1/3pi"R"^2H`
`=1/3pi(2"r")^2xx(2"h")` [Using (i) and (ii)]
`= 8/3pir^2h`
so, Volume frustum = Volume of solid cone - Volume of smaller cone
`= 8/3pi"r"^2"h" - 1/3pi"r"^2"h"`
`=7/3pi"r"^2"h"`
Now, the ratio of the volumes of the two parts `= "Volume of the smaller cone"/"Volume of the frustum"`
`=(1/3pi"r"^2"h")/(7/3pi"r"^2"h")`
`=1/7`
= 1 : 7
So, the ratio of the volume of the two parts of the cone is 1 : 7.
APPEARS IN
संबंधित प्रश्न
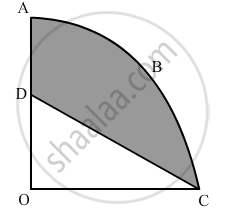
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct upto one place of decimal?
Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
A golf ball has diameter equal to 4.2 cm. Its surface has 200 dimples each of radius 2 mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.
The surface areas of two spheres are in the ratio of 4 : 25. Find the ratio of their volumes.
Choose the correct answer of the following question:
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
Arrange the given objects according to their volume
What is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
