Advertisements
Advertisements
प्रश्न
A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.
उत्तर
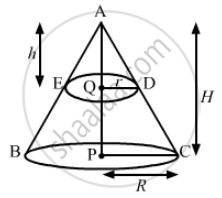
We have,
Radius of solid cone, R = CP = 10 cm,
Let the height of the solid cone be, AP = H,
the radius of the smaller cone, QD = r and
the height of the smaller cone be, AQ = h.
Also, `"AQ"= "AP"/2 "i.e" "h"="H"/2 or "H = 2h" .......(i)`
Now, in Δ AQD and Δ APC
∠QAD = ∠PAC (Common angle)
∠AQD = ∠APC = 90°
So, by AA criteria
ΔAQD ˜ ΔAPC
`⇒ ("AQ")/("AP") = ("QD")`
`rArr "h"/"H" = "r"/"R"`
`rArr "h"/"2h" = r/"R"` [Using (i)]
`rArr 1/2 = "r"/"R"`
`rArr "R" = 2"r"` ..............(ii)
As,
Volume of smaller cone `= 1/3 pi"r"^2"h" `
And,
Volume of solid cone `= 1/3pi"R"^2H`
`=1/3pi(2"r")^2xx(2"h")` [Using (i) and (ii)]
`= 8/3pir^2h`
so, Volume frustum = Volume of solid cone - Volume of smaller cone
`= 8/3pi"r"^2"h" - 1/3pi"r"^2"h"`
`=7/3pi"r"^2"h"`
Now, the ratio of the volumes of the two parts `= "Volume of the smaller cone"/"Volume of the frustum"`
`=(1/3pi"r"^2"h")/(7/3pi"r"^2"h")`
`=1/7`
= 1 : 7
So, the ratio of the volume of the two parts of the cone is 1 : 7.
APPEARS IN
संबंधित प्रश्न
Water flows at the rate of 10 m / minute through a cylindrical pipe 5 mm in diameter . How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm.
A factory manufactures 120,000 pencils daily . The pencil are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm . Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm2.
Two cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each hemispherical end is 7 cm, find the surface area of the solid.
A sphere and a cube have equal surface areas. The ratio of the volume of the sphere to that of cube is ______.
The circumference of the front wheel of a cart is 3 m long and that of the back wheel is 4 m long. What is the distance travelled by the cart, when the front wheel makes five more revolutions than the rear wheel?
The radius of a metallic sphere is 8 cm. It was melted to make a wire of diameter 6 mm. Find the length of the wire.
Find the surface area of a sphere of radius 7 cm.
Solution :
The surface area of the sphere = 4πr2
= `4 xx 22/7 xx square^2`
= `4 xx 22/7 xx square`
= `square xx 7`
∴ The surface area of the sphere = `square` sq.cm.
